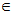[xi,xi+1] with y=G’ and y=G” through the neighboring points.
The cross point is defined as the intersection of the G’ and G” lines as a function of x. The crossover point is calculated from two curves fitted to the neighborhood of the crossover. Two interpolation techniques can be used; linear interpolation of the two neighboring points of each curve or a cubic spline to fit the points of each curve in the neighborhood of the crossover. X can be either frequency, time, strain, etc.
The linear interpolation uses a line fit y(x)=ax+b with y=G’ and G” through the two neighboring points only.
The cubic spline uses a cubic fit yi(x)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3 for x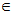[xi,xi+1] with y=G’ and y=G” through the neighboring points.
The interpolation technique can be selected on the ‘Input parameters’ tab of the Function Settings.
Selections are: 1. Linear, 2. Cubic Spline, 3. Linear/cubic spline combination.
Use the Crossover point analysis option to determine the point at which G’=G” or tand=1. This can be the crossover point in a frequency sweep (i.e., elastic to viscous response), a strain sweep (i.e., linear to non-linear behavior), a time sweep (i.e., gel point).
